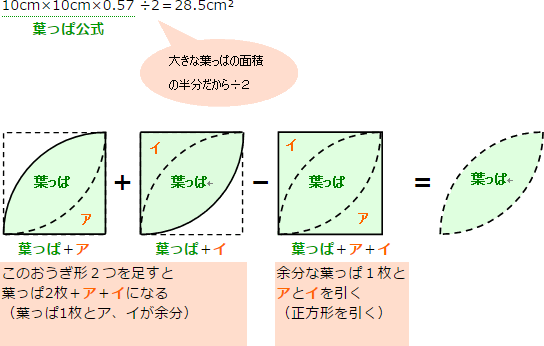
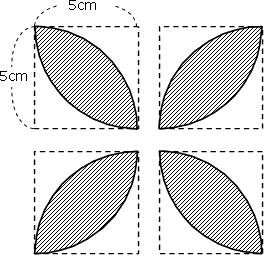
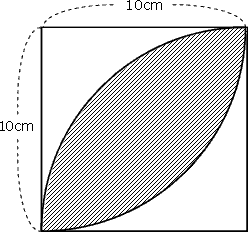
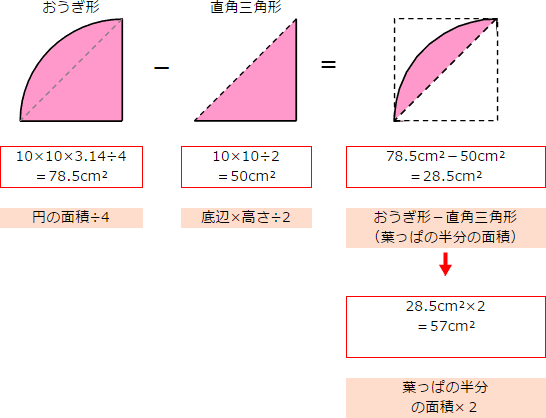
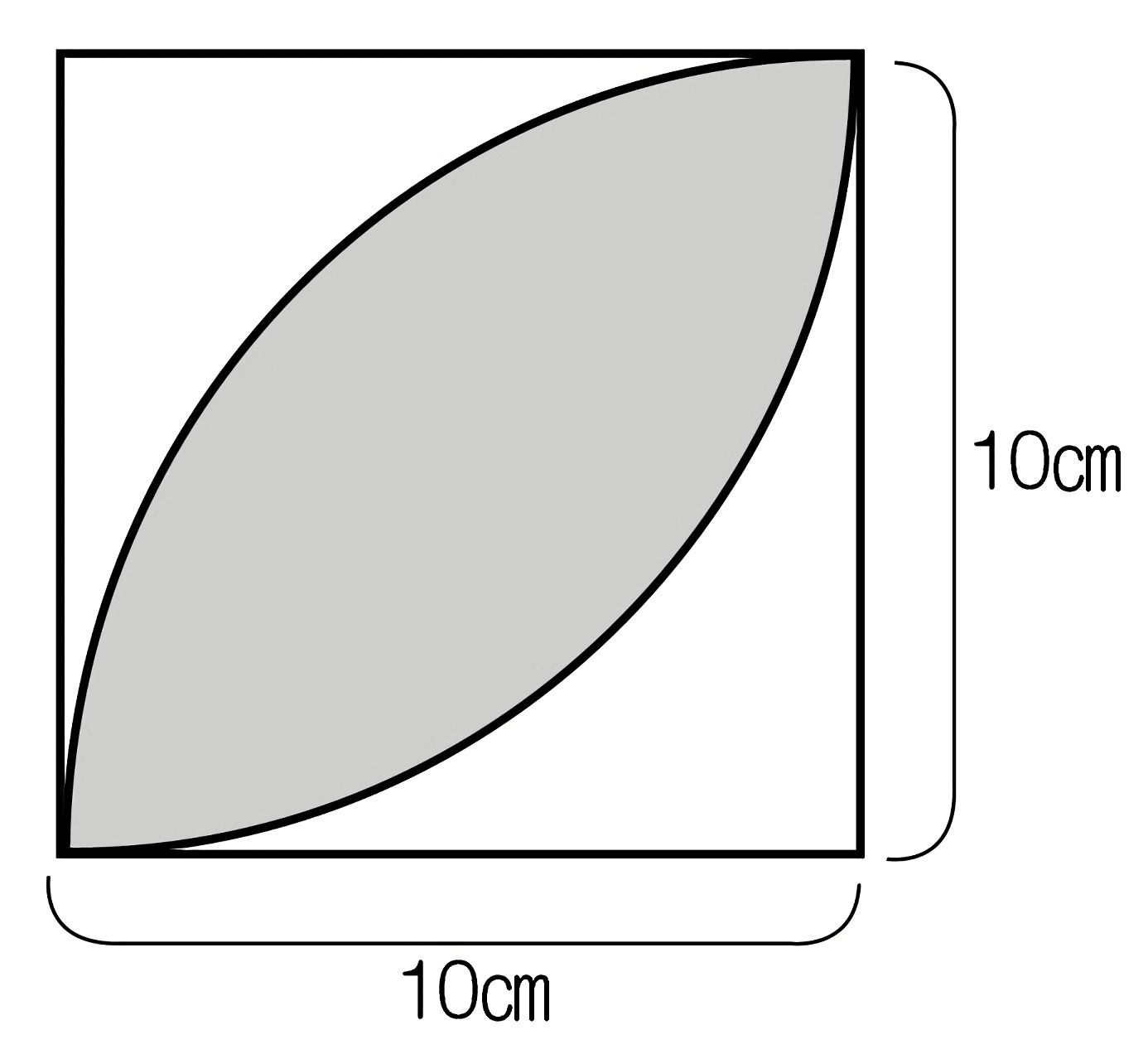
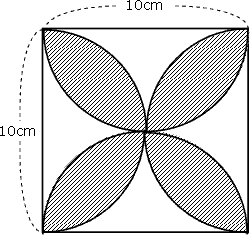
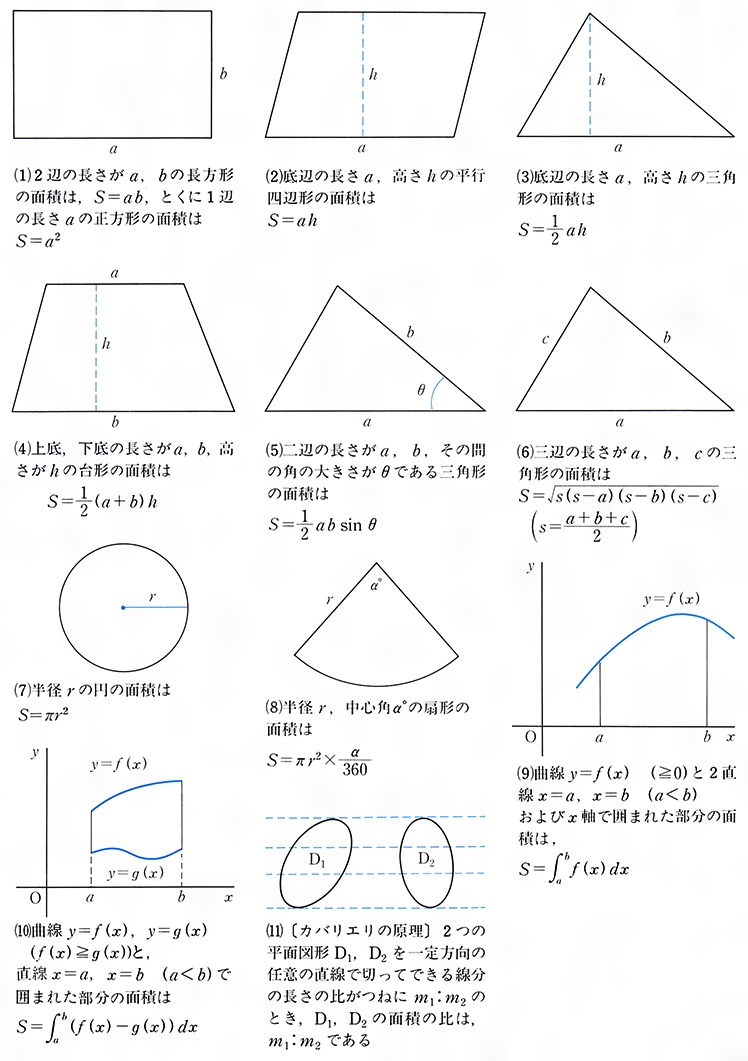
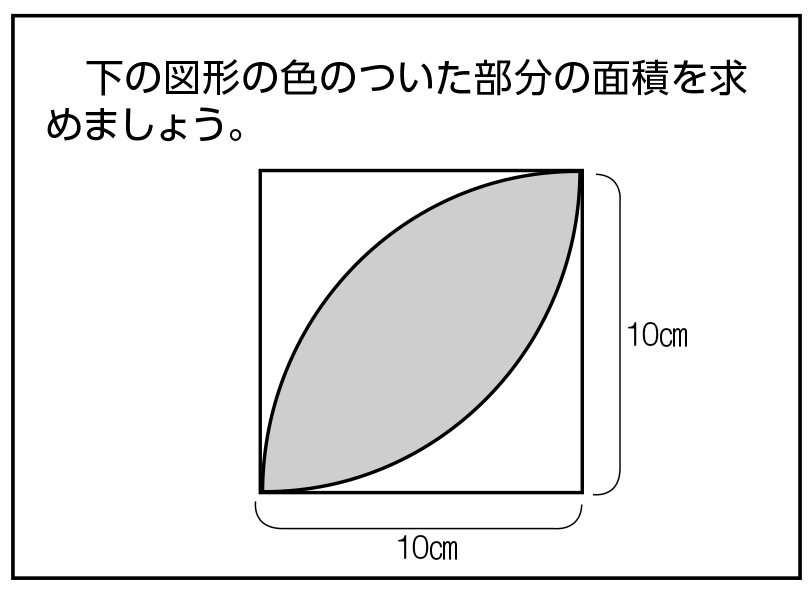
底面積の求め方 図形ごとの底面積の求め方の一覧を下記に示します。 立方体 ⇒ 縦×横 直方体 ⇒ 縦×横 円柱 ⇒ 半径×半径×314 四角柱 ⇒ (上底下底)÷2×高さ 三角柱 ⇒ 底辺×高さ÷2 円錐 ⇒ 半径×半径×314 四角錐 ⇒ (上底下底)÷2×高さ13/6/ ひし形(対角線直交四角形)の面積=対角線×対角線÷2 円周=直径×円周率(314)=半径×2×円周率(314) 円の面積=半径×半径×円周率(314) おうぎ形の弧の長さ=円周×中心角/360=直径×314×中心角/36013/9/05 つまり、葉っぱ型の図形の面積は (1辺の長さ)×(1辺の長さ)×057 でもとめることができるのです。 この公式を覚えておくと、問題を効率よく解くことができます。 ただし、円周率が314とした場合のみにあてはまる公式です。

5年生で 様々な図形の面積の求め方を習いますが ここでは 平行四辺形と三角形の面積の求め方を学習する自主学習ノートの例を紹介します 平行四辺形と三角形の面積を求める 三角形の面積 子どもたちの研究 学習 学習ノート
図形の面積の求め方 小学生
図形の面積の求め方 小学生-15/5/15 中学数学3分で簡単にわかる!「扇形(おうぎ形)の面積の求め方」の公式 中1数学 平面図形5ステップでできる!点対称移動の作図・書き方 中3数学 3秒で計算!?長方形の対角線の求め方がわかる公式 中1数学25/6/ 図形の面積の求め方のテクニック! この記事では、図形の面積を求める際に必要な考え方・ テクニックを簡単にまとめます。 図形の公式等、平面図形の面
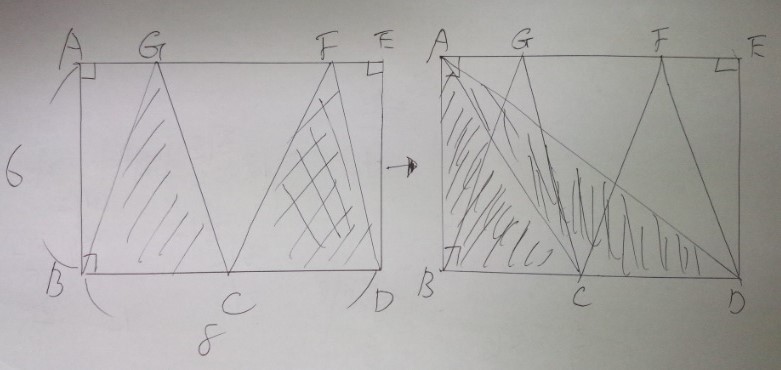



図形の面積の求め方のテクニック 基本編 中学受験 塾なし
12/7/05 つまり,上半分の長方形の面積をたて×よこで計算してから, おうぎ形(灰色) の面積を計算して,引き算をすれば, 黄色の図形 の面積を求めることができるのです。三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。 基本的な面積の求め方・公式を解説 それでは早速、四角形や長方形の基本的な面積の求め方・公式からみていきましょう。 三角形の面積 三画形の面積 は、 底辺×高さ÷2 で求めることができます。 三角形は平行四辺形を対角線で切って半分にした形 です。
教え方1 平行四辺形の面積の求め方 その前に4年の面積の求め方の勉強を思いたださせたいと思います。 下の複合図形の面積を求めるには、 長方形や正方形 の形に おきかえて 面積を求めたことをふりかえらせて下さい。三角形、四角形、角、面積 円、三角形、四角形の面積を計算できるようになろう。 角度のはかり方もいっしょにおぼえてね。 動画で学ぼう! (NHK for School) 三角形の面積の求め方を、四角に直すことで原理から考える。 結婚式場から指輪が盗まれた5/6/21 円環の面積の求め方は下記の通りです。 円環の中心から外側の円での半径をR、内側の円の半径をrとした場合 円環とは、ドーナツ形とも呼ばれ、中心が同じ大きさの異なる円によってできた図形をいいます。 7楕円 楕円の面積の求め方は下記の通りです。
台形の1辺・面積(3辺の長さと高さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 ひし形の面積 平行四辺形の面積 (底辺と高さから) 平行四辺形の面積(底辺と高さから) 平行四辺形の面積 (2辺と夾角から)及び長方形の面積の求め方について考え、面積を求める公式を用いて複合図形や大きな単位の面積の求 め方を考えていく。 この学習は第5学年の直方体や立方体などの体積や、平行四辺形や三角形などの面積を求める学習へ とつながっていく。 児童観1 提示した図形の面積の求め方を調べる。 〇 長方形の縦と横の辺の長さに着目し、「底辺×高さ÷ 2」という求積公式を捉えること 1 底辺と高さと面積の関係を調べる。 〇 底辺をどこにとっても、底辺と高さの垂直関係に着目




はっぱ型 の図形の面積 身勝手な主張




平面図形の苦手を解消 三角形の面積比 基本編
314×1=314 314×2=628 314×3=942 314×4=1256 314×5=157 314×6=14 314×7=2198 314×8=2512 314×9=264年算数 大きい面積の求め方 子どもの学習支援 by いっちに算数 スマホ版 前のページに戻る 教え方4 平方メートル の単位を教え、平方メートル と平方センチメートル の単位の関係に気づかせます。 そのあとで、㎝とmの単位を混合した正方形や長方形の面積を求める問題を考えさせます。Hello School 算数 体積・表面積 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。



Spi M54e217p7lcis9d Com Category E5 9b E5 81 Ae E9 9d E7 8d
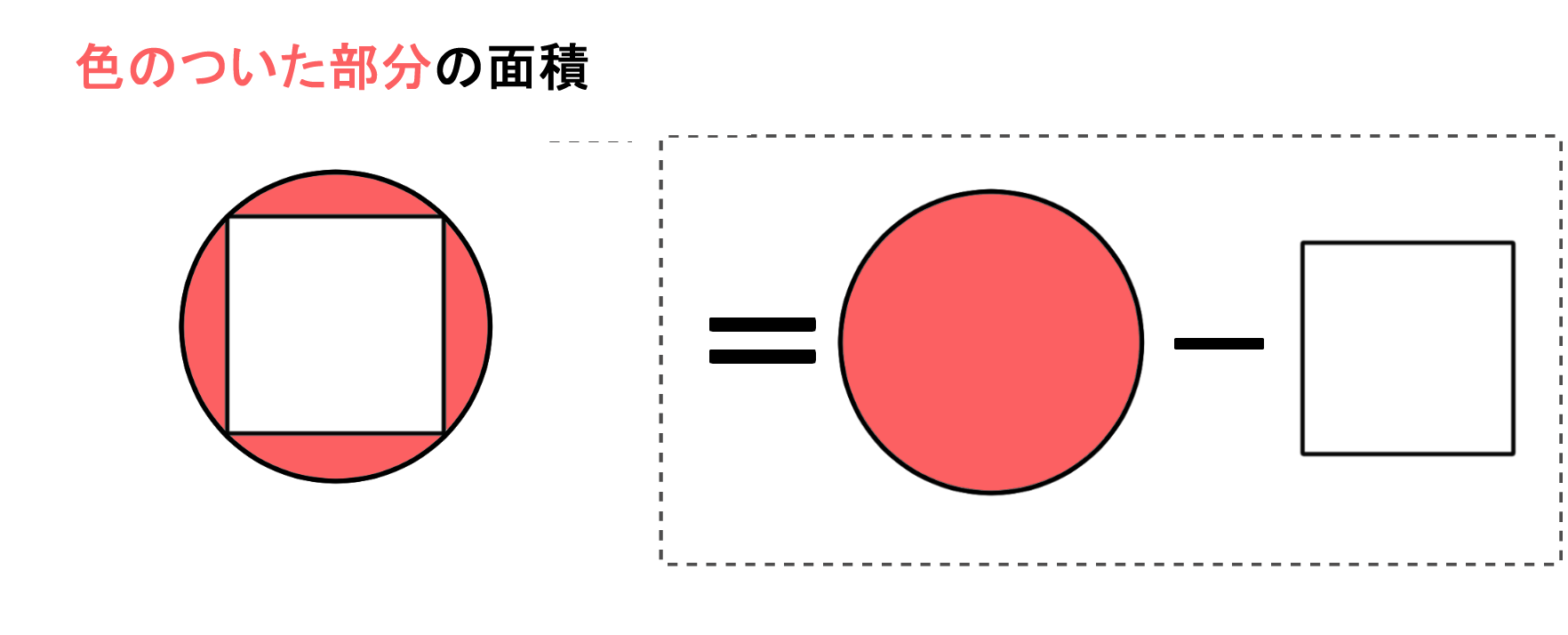



色のついた部分のへんな形の図形の面積を求める問題 バカでもわかる 中学数学
面積を求めるには、図形の幅と高さ(別の言い方をすれば、接する2辺の長さ)を知る必要があります。 1 X 出典文献 平行四辺形の面積を求めるには、底辺とそこから垂直に伸びる高さを知る必要がありますが、基本的には幅と高さと同じように考えます。表面積 = 半径 × 半径 × 314 半径 × 母線の長さ × 31416/3/15 「 おうぎ形の面積の求め方 」はつぎの公式であらわされるんだ。 半径をr、面積をS、円周率をπ、中心角をαとすると、 S = πr² × α / 360



小5算数の問題です 色付き部分の面積の求め方をわかりやす Yahoo 知恵袋




図形の面積の求め方のテクニック 基本編 中学受験 塾なし
平面図形 例題 基本の作図(垂線) 基本の作図(垂直二等分線、角の二等分線) 作図 正三角形,円の中心 作図 角度60°,30°,45° 作図 角度75° 作図 平行線 円の接線 作図 三角形の3頂点を通る円, 三角形の3辺に接する円 おうぎ形_半径と中心角から弧の長さや,面積を求める おうぎ形2_半径と弧から,面積を小学校学習指導要領・算数の第5学年では,内容「B量と測定」「 (1)図形の面積を計算によって求めることができるようにする。 ア 三角形,平行四辺形,ひし形及び台形の面積の求め方を考 えること」を示している。 また,「 算数的活動 (1)イ 三角形,平行四辺立体の体積 → 携帯版は別頁 曲線で囲まれた図形の面積 区間 a≦x≦b において,つねに f (x)≧g (x) であるとき,2つの曲線 y=f (x), y=g (x) と直線 x=a, x=b とで囲まれる図形の面積は S= b∫ awww { f (x) − g (x) }dx (1) ※ (上) - (下) の積分 と考える




平行四辺形の面積の求め方 公式と計算例
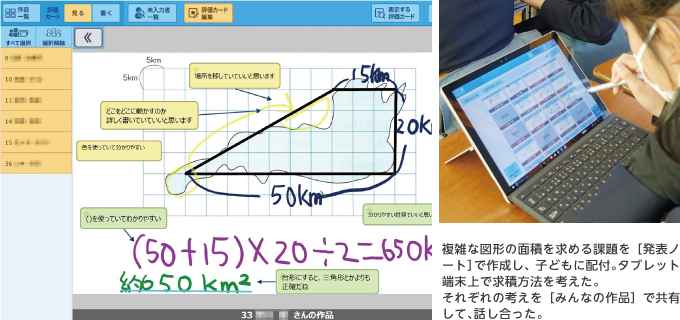



茨城大学教育学部附属小学校 学校とict sky株式会社 Ictを活用した学習活動をサポート
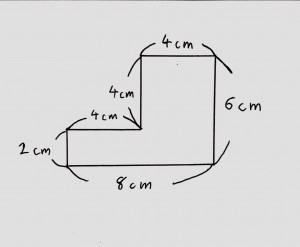
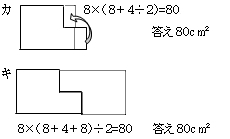
本単元は、図形を分解したり合成したりする具体的な操作 (等積変形や倍積変形)を通して,平行四辺形、三角形、台形、ひし形の面積の求め方を考え、それらの公式をつくるとともに、その公式を用いて面積を求めることができるようにすることがねらいである。 台形の面積を求める時間としては、前時と本時の2時間を使う。 前時では、台形を等積変形や倍図のような曲線 y = f (x) と x 軸,および 2直線 x = a ,x = b で囲まれた図形の面積 S は定積分を利用して, で求められます。ここはわかっているようですね。 この を計算すると,負になってしまったのですね。 面積ですから負になるのはおかしいです。18/3/21 それぞれの長方形を求めて、全て足せば面積を求めることができるので、式は、 4×4+4×3+(84)×10=68 よって、 答え 68㎠ 例題2 下の図をように、長方形の中に、たてと横に幅2cmの隙間を作りました。このときの面積を求めなさい。




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



この四角形の中の三角形の面積の求め方をおしえてください A 長方形 Yahoo 知恵袋
6/3/21 三角関数sinを用いた三角形の面積 られているときは(ヘロンの公式を用いてもよいですが),余弦定理を用いてコサインを求め 5 円周率100桁の覚え方を教えてください! 5028三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から)7角形の面積を求めてみよう。 計算上、最後の3角形の面積計算のため、1番目の点座標を8番目にも設定します。 図4 多角形(ポリゴン)の面積を求めるエクセルシート 簡単ですね。




円周の求め方の基本問題が解けるようになったら 次は応用問題にも挑戦してみましょう これも 5年生後半から6年生向けの内容です 円周の長さを求める応用問題を解こう 円周の長さを求める問題で もっと基本 数学ノート 学習 学習ノート




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ
小学5年生の算数立体の体積の求め方練習プリントを無料ダウンロード・印刷 (プリント5枚) 小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題図形の面積の求め方 A=面積 A=s 2 A=1/2d 2 S= d= d=1414 s=1414 A=面積 =弧の長さ a=角度 A=面積 A=面積 =弧の長さ a=角度A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台
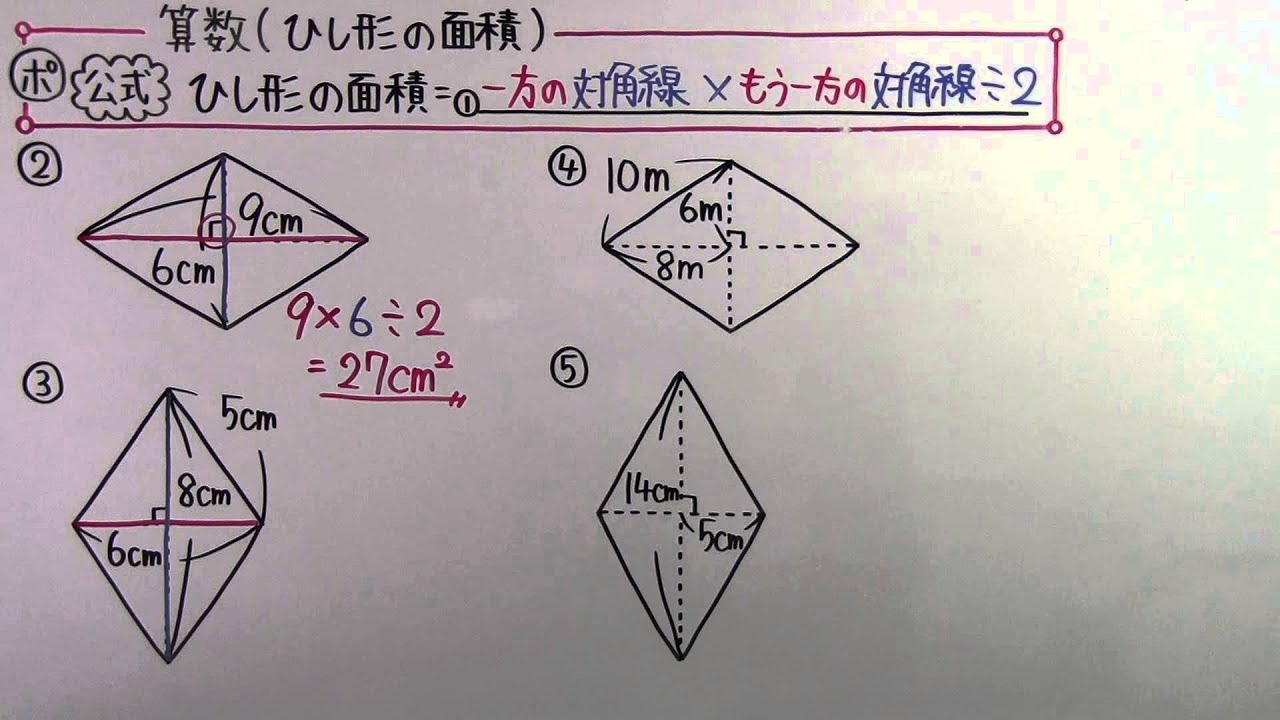



小5 算数 小5 44 ひし形の面積 Youtube




この図形の面積の求め方を教えてくださいm M Clear
三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。次に、下側 (オレンジ)の面積を求めていきますが、求めたい面積の図形は台形となっています。 (台形の面積は「 (上辺下辺)×高さ÷2」で求められます。長方形の面積 縦 たて ×横 よこ =面積 めんせき a×b =a b 正方形の面積 一辺 いっぺん ×一辺 いっぺん =面積 めんせき a×a=a2 三角形の面積 底辺×高さ÷2=面積 a×h 2 1 a h 台形の面積
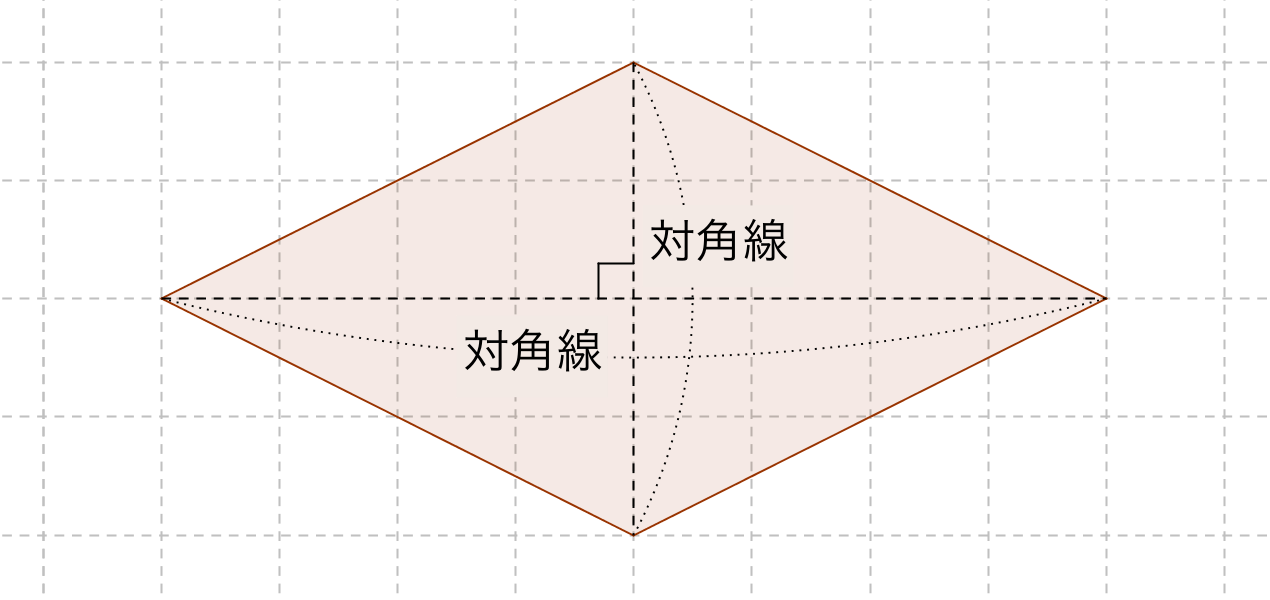



ひし形の面積の公式 算数の公式



1
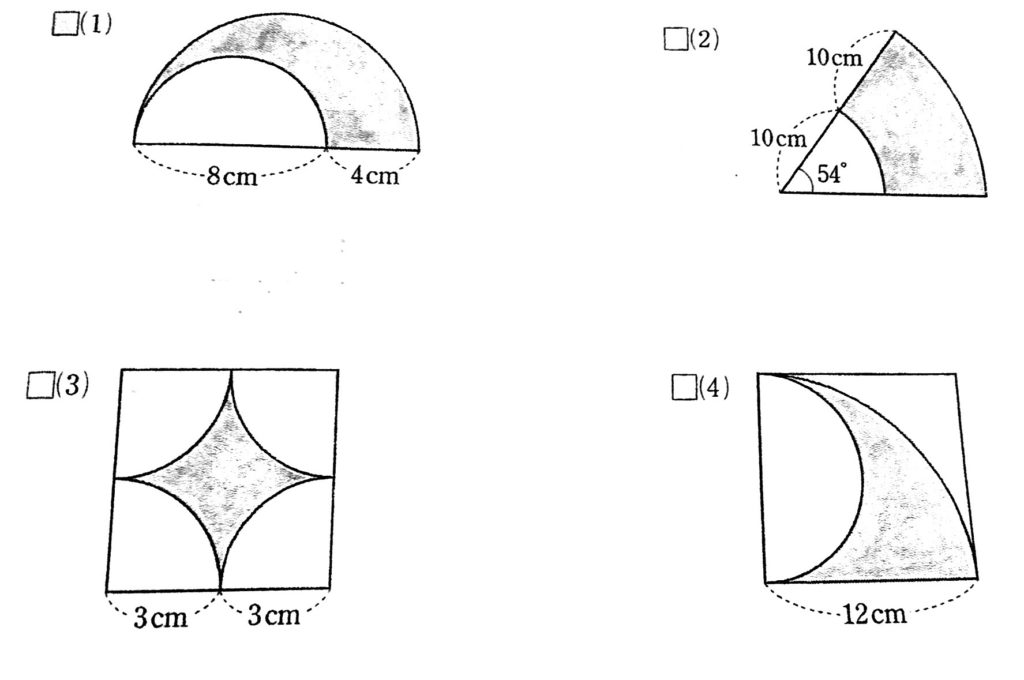



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ
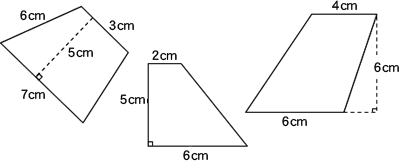



図形の面積 面積の求め方を考えよう 第5学年 小学校 算数 My実践事例 日本文教出版
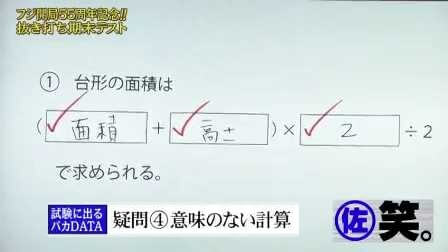



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師



面積の求め方




小学5年生 算数 11月 台形の面積 いろいろな図形の面積 割合 百分率の意味と求め方 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ



1
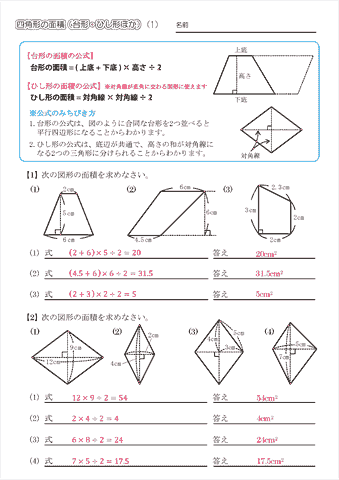



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生




算数 小4 41 面積の求め方のくふう Youtube




いろいろな面積を求める問題1 中学受験準備のための学習ドリル




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト




小学5年生 算数 11月 台形の面積 いろいろな図形の面積 割合 百分率の意味と求め方 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ
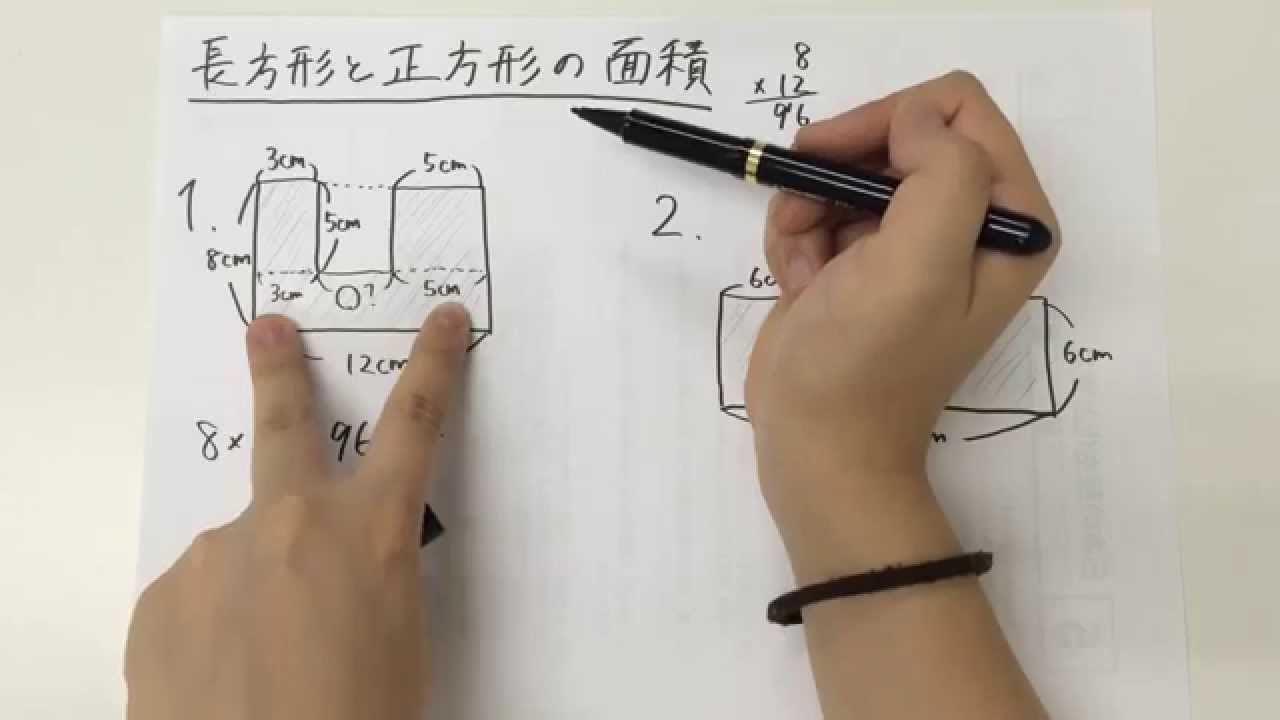



4年生 10 長方形と正方形の面積の求め方 Youtube




5年算数面積 教え方のポイント
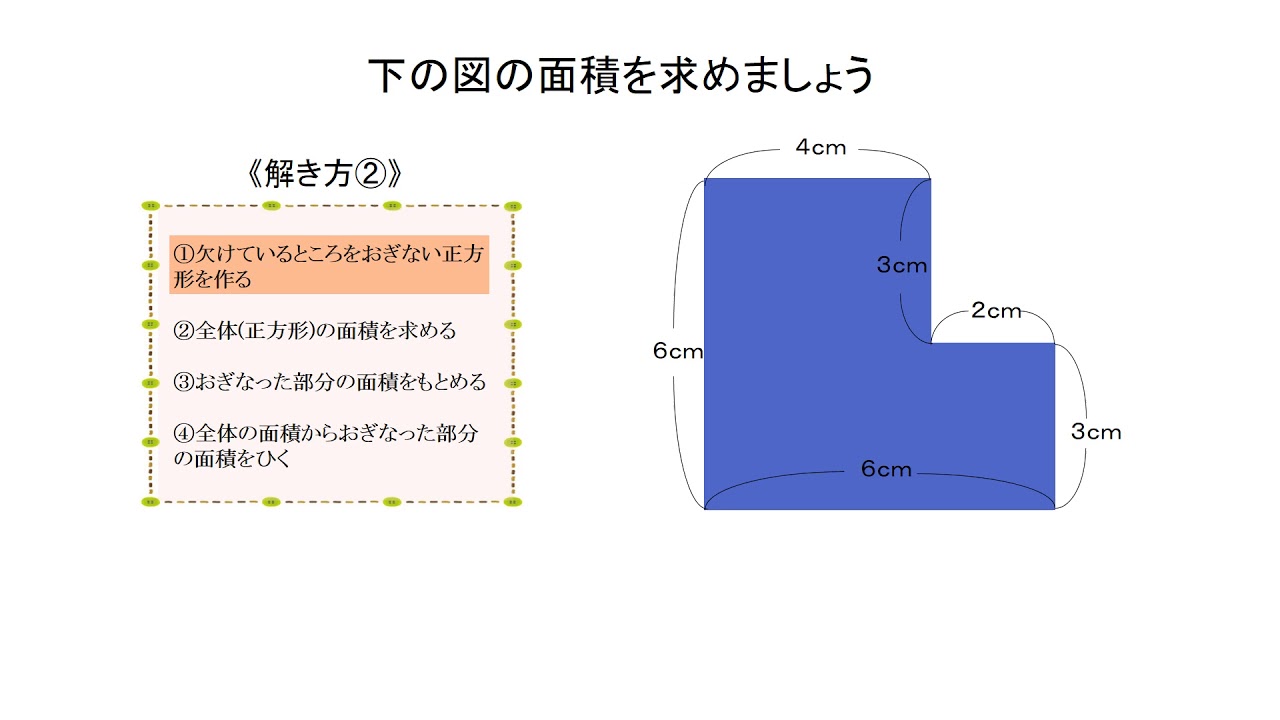



小4 面積の求め方の工夫 日本語版 Youtube
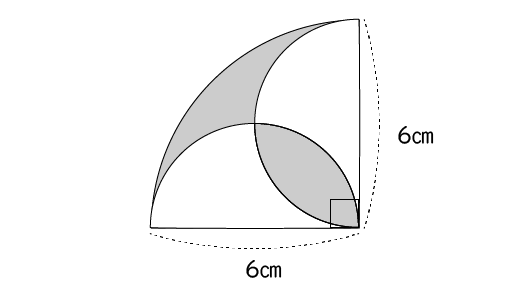



中学1年生数学 複雑な面積の求め方 長野地区 Itto個別指導学院 長野市の学習塾



面積の求め方 算数の教え上手 学びの場 Com



小学校で習うひし形の面積の求め方 対角線を使った公式で求められる理由 みけねこ小学校




三角形の成立条件と面積の求め方を解説 図形と方程式




平行四辺形の面積の求め方 公式と計算例



面積 体積を求める問題が苦手な子へ 小学生向け 愛知 岐阜の個人指導専門塾



面積の求め方 算数の教え上手 学びの場 Com




高校数学b 三角形の面積のベクトル表示 成分表示とその証明 受験の月




平面図形の面積の求め方 基本編 中学受験 塾なし の




正方形 長方形の面積の求め方 小学生に教えるための分かりやすい解説 数学fun



面積の求め方 算数の教え上手 学びの場 Com
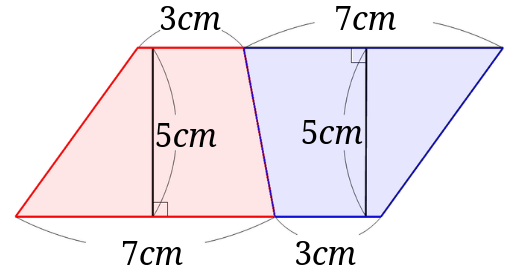



台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校
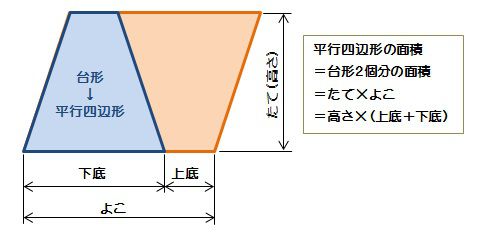



台形の面積 算数の公式覚えてますか




長方形の面積の求め方 簡単な計算問題で公式を覚えよう 中学や高校の数学の計算問題




面積の求め方 算数の教え上手 学びの場 Com
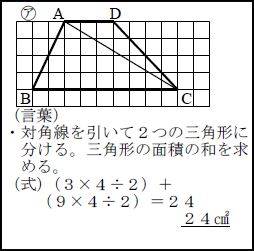



私の実践 私の工夫 算数 第5学年 面積 台形 啓林館
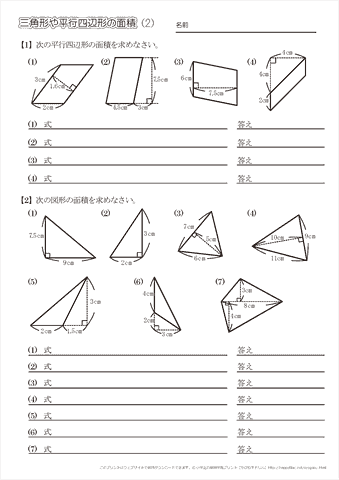



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく
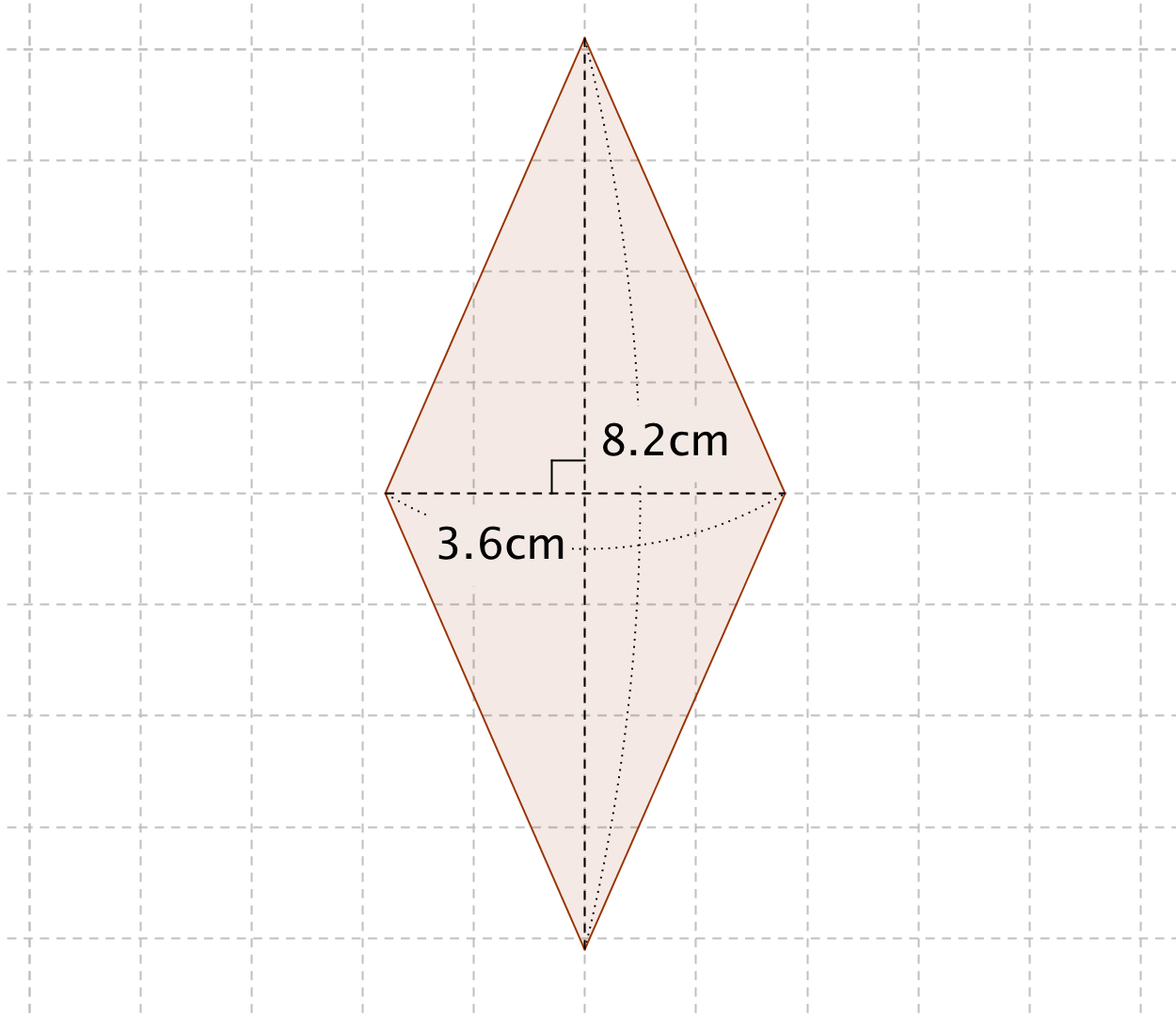



ひし形の面積の公式 算数の公式
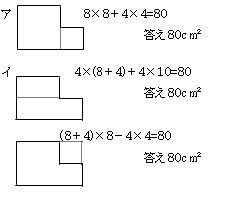



実践記録算数4年




数学の図形の面積についてです 画像の色のついた部分の面積の求め方 数学 教えて Goo




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
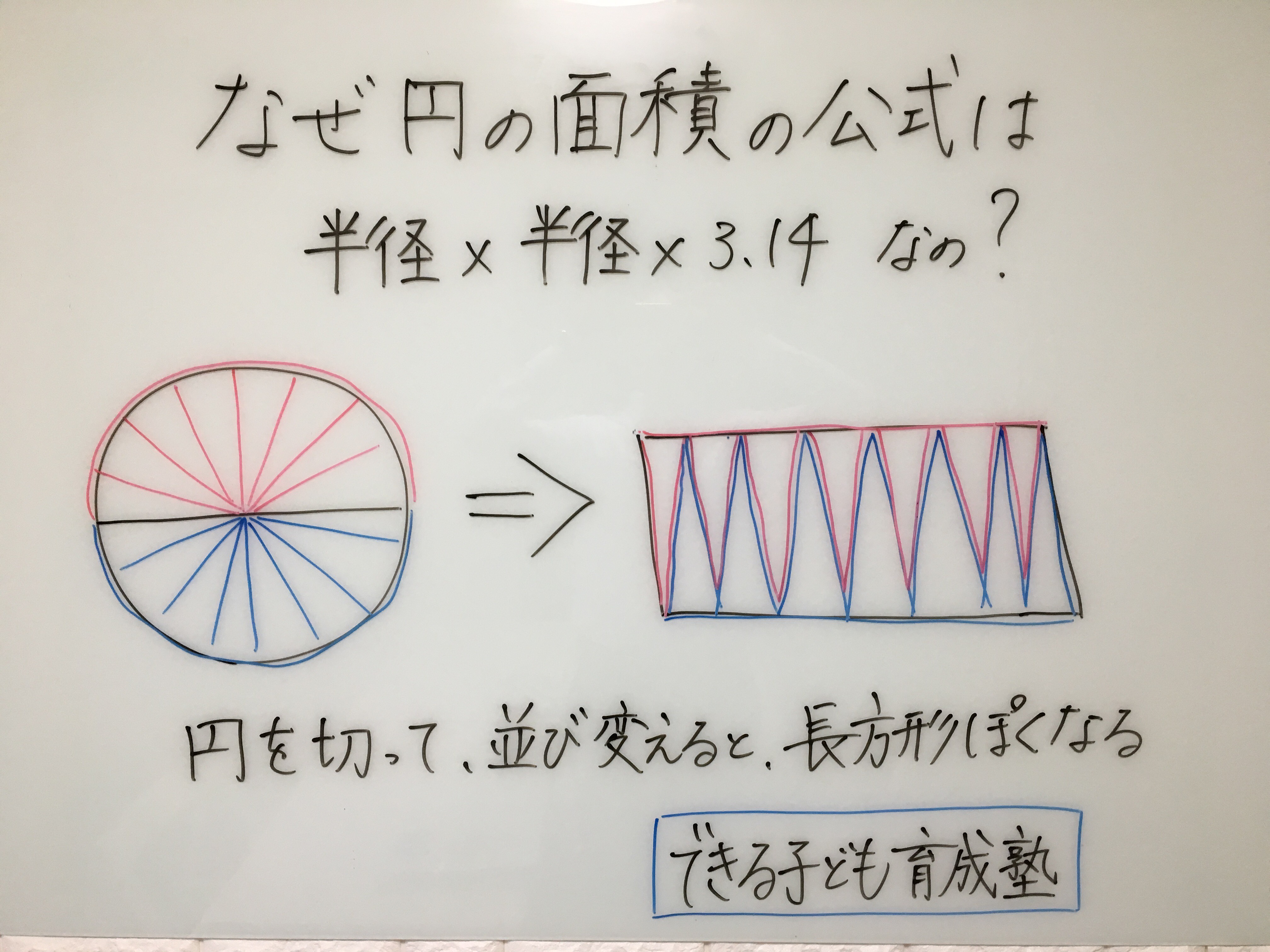



円の面積の求め方 公式 の理由を小学生に教える方法 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服



教育ソフト開発研究所 5年5巻




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




ひし形 菱形 の面積の公式は 対角線 対角線 2 見やすい図で即理解 高校生向け受験応援メディア 受験のミカタ



Q Tbn And9gcqzeeo01vtcqismk0aakbfqlilzl1ycybvocm32kspywiawohri Usqp Cau




小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題



面積の求め方 算数の教え上手 学びの場 Com




平行四辺形の面積の求め方 公式と計算例




5年生で 様々な図形の面積の求め方を習いますが ここでは 平行四辺形と三角形の面積の求め方を学習する自主学習ノートの例を紹介します 平行四辺形と三角形の面積を求める 三角形の面積 子どもたちの研究 学習 学習ノート



実践記録算数4年




写真のような図形の面積の求め方で 四角形から引くやり方以外で解き方はありますか Clear




円の面積の求め方を一通り身につけたら 少し応用的な問題にも挑戦してみましょう 円の面積の応用問題をやってみよう 円の面積の もっと基本的な問題のノート例はこちらです 円の面積 数学ノート 学習ノート 学習




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
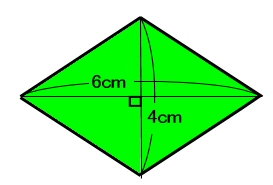



ひし形の面積の求め方




算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素




小6算数 円の面積 指導アイデア 2 みんなの教育技術




台形の面積の公式 ゆとり教育で求め方がわからない人は見て 中学や高校の数学の計算問題




ひし形の面積の公式 面積の求め方は対角線に注目しよう 中学や高校の数学の計算問題



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト




面積の求め方 計算公式一覧




面積の求め方 計算公式一覧



2直角四角形の面積を求める極意 すぐるゼミ
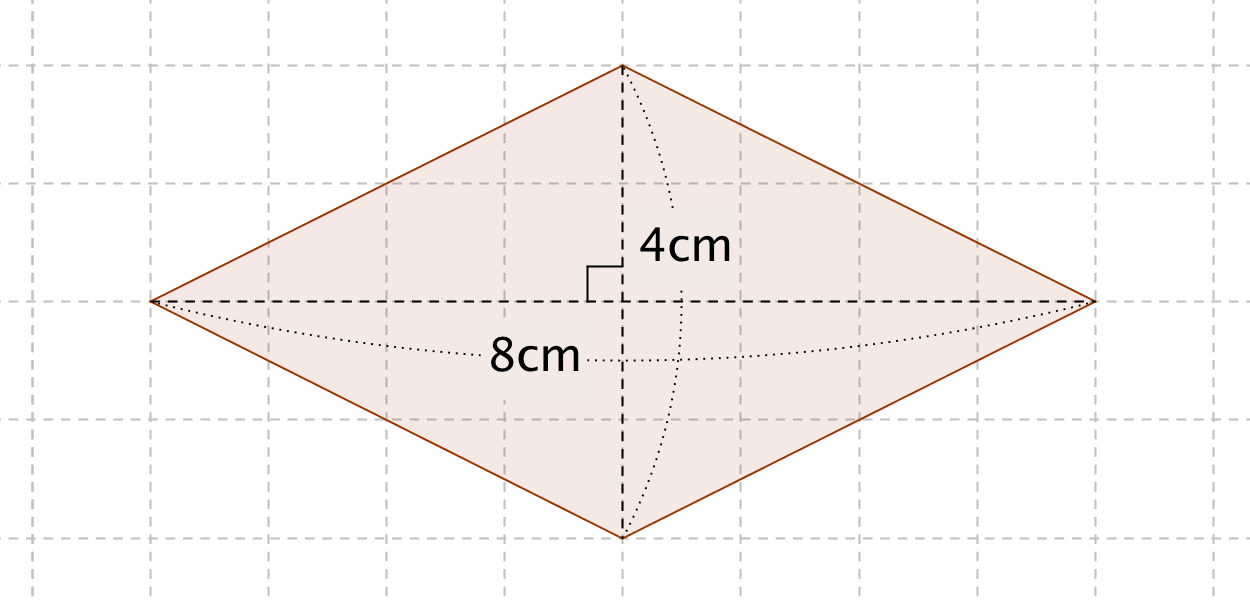



ひし形の面積の公式 算数の公式




面積の求め方 算数の教え上手 学びの場 Com
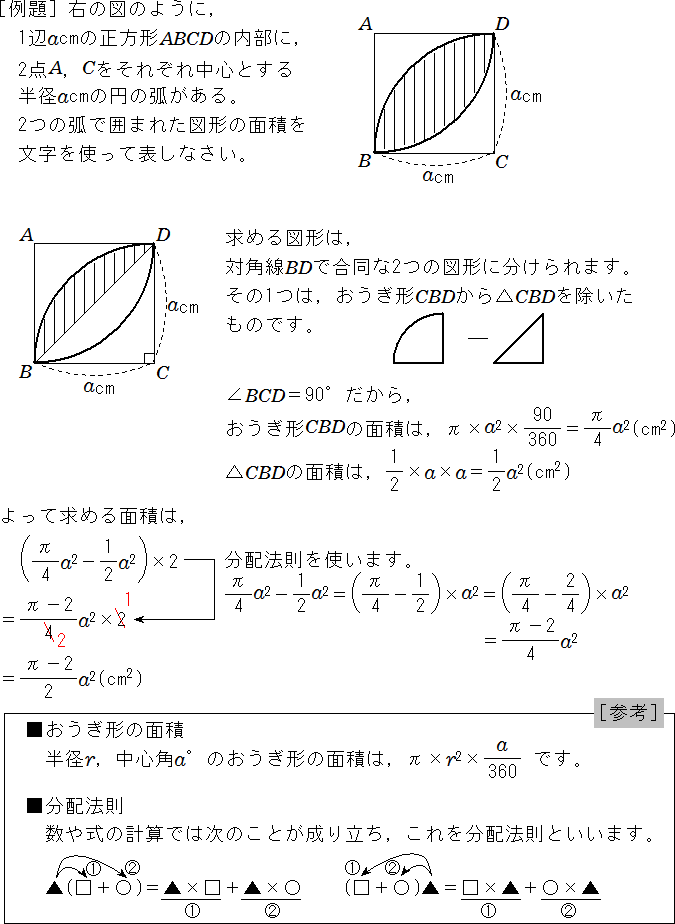



式の計算 文字を使った変わった図形の面積の求め方 中学数学 定期テスト対策サイト




台形の面積の求め方 公式と計算例



1




面積の求め方 公式一覧 小学生 中学生の勉強




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題
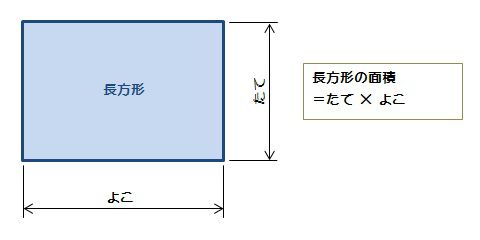



長方形の面積 算数の公式覚えてますか




小5算数 図形の面積 指導アイデア みんなの教育技術
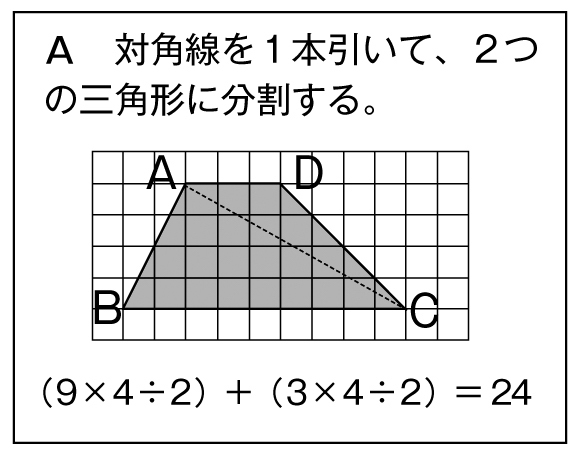



小5算数 図形の面積 指導アイデア みんなの教育技術
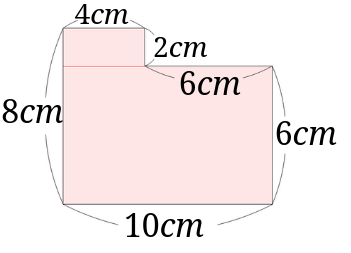



小学4年生で習う長方形や正方形の面積の応用問題を解説 みけねこ小学校




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



小6算数 円の面積 指導アイデア 2 みんなの教育技術




公式なんて覚えない ひし形の面積は直感的に考えよう




小5 面積 三角形の面積の求め方 日本語版 Youtube




円の面積 練習応用 Youtube



面積の求め方 算数の教え上手 学びの場 Com




三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




標準 おうぎ形と正方形の面積 なかけんの数学ノート




小6 算数 小6 2 円の面積 応用編 Youtube
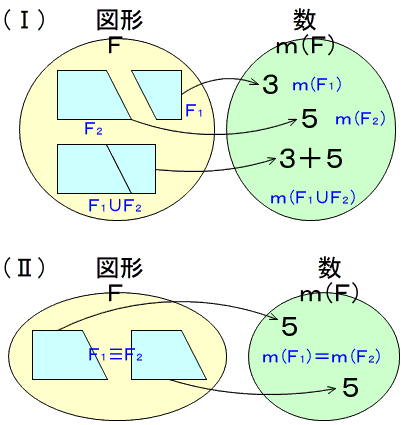



長方形の面積を求める公式の数学的な意味 Note Board




平行四辺形の面積の求め方 公式と計算例




この図形の面積の求め方を教えてください お願いします この図形 小学校 教えて Goo
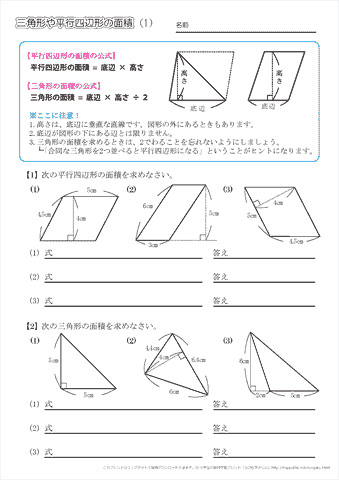



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



面積とは コトバンク



小6算数 円の面積 指導アイデア 2 みんなの教育技術



0 件のコメント:
コメントを投稿